1D - Tracer transport dual porosity during transient flow simulations
Problem Definition
This example describes the transport of two tracers under transient flow conditions in a one-dimensional profile. One tracer (tracer A) is added as a pulse in the infiltrating water (boundary value problem); the other tracer (tracer B) is initially present in the immobile domain of the problem. Water flow and solute transport are described with the dual-porosity model with both exchange of water and solutes between the mobile and immobile domain. The aim is to verify the coupling of HYDRUS-1D and PHREEQC.
Acronym: ADR-DP-Transient
Geometry
The profile has a length of 100 cm and consists of a single material.
Processes and Equations
|
Water flow equation |
vertical flow (α=1), no water sink (S=0) |
|
|
Solute transport |
|
Initial and boundary conditions
The initial and boundary conditions are illustrated in Figure 1.
Figure 1 - Schematic representation of initial and boundary conditions for water flow (left) and solute transport (right)
The upper boundary water flow conditions consists of daily precipitation and evaporation rates for 300 days.
The upper boundary condition for mass transport is a time-variable flux boundary condition with
|
cA |
0.1 mmol/kgw |
0 ≤ t ≤ 53d |
|
|
0.0 mmol/kgw |
53 ≤ t ≤ 300d |
|
cB |
0.0 mmol/kgw |
|
Material Parameters
The hydraulic properties are described with the van Genuchten - Mualem model with m=1-1/n. Parameter values are in Table 1.
Table 1 - Parameters of the moisture retention curve and the unsaturated hydraulic conductivity as described with the model of van Genuchten -Mualem.
(θs,im and θi,im are the saturated and residual water content of the immobile regions [-], and ω is the mass transfer coefficient)
|
θs |
0.43 |
|
θr |
0.078 |
|
α |
0.036 /cm |
|
n |
1.56 |
|
Ks |
24.96 cm/days |
|
l |
0.5 |
|
θs,im |
0.1 |
|
θr,im |
0 |
|
ω |
0.01 1/days |
The parameters of the solute transport equation and dispersion are given in Table 2.
Table 2 - Parameters of the solute transport equation (dual-porosity non-equilibrium advection-dispersion equation)
|
DL |
8 cm |
|
Dw |
0 cm2/day |
|
τ |
|
|
ω |
0.005 1/day |
Evaluation method
HPx simulations are compared with the calculations results of HYDRUS-1D. The output variables are:
- Time series of concentration of Tracer A and B in the mobile region at depths of 3, 25, 50, 75, and 100 cm.
- Profiles of concentration of Tracer A and B in the mobile region, immobile region and total soil at 10, 30, 50, 100, 200 and 300 days.
Numerical Settings
The profile is discretized in 100 elements with 101 equally-spaced nodes.
The minimum and maximum time steps are 10-5 and 1 days, respectively.
The Crank-Nicholson scheme for time weighting and the Galarkin finite element scheme for space weighting are used with a stability criterion (PeCr) equal to 2.
Results
Figure 2 shows an excellent agreement between the time series of aqueous concentration of Tracer A and B obtained with HYDRUS-1D and HPx at selected depths.
Figure 3 shows an good agreement between profiles of Tracer A and B at selected times obtained with HYDRUS-1D and HPx.
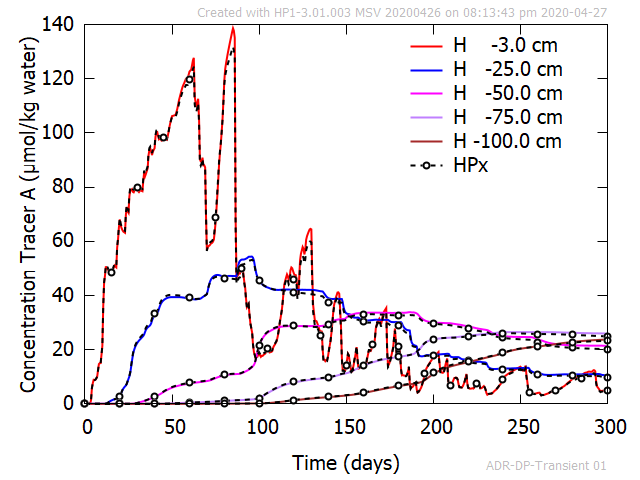
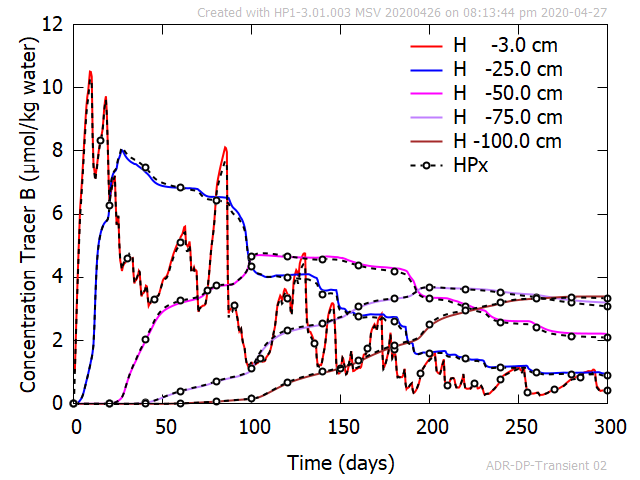
Figure 2 - Time series of aqueous concentrations of Tracer A and B in the mobile region. Comparison between HPx and HYDRUS-1D.
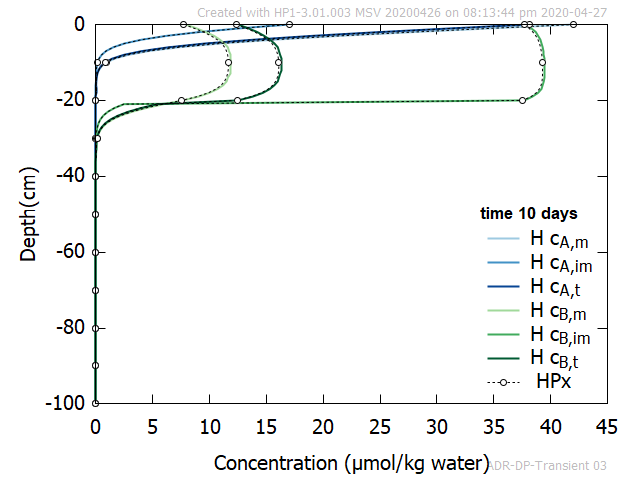
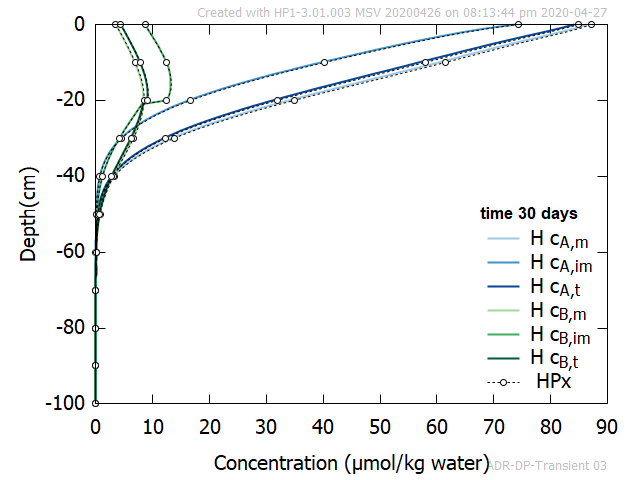
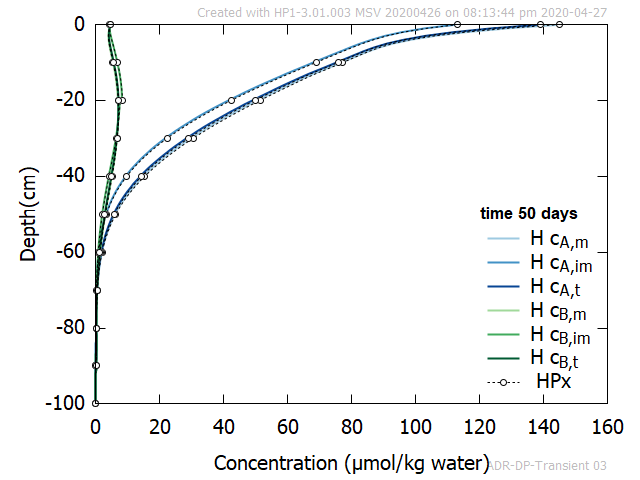
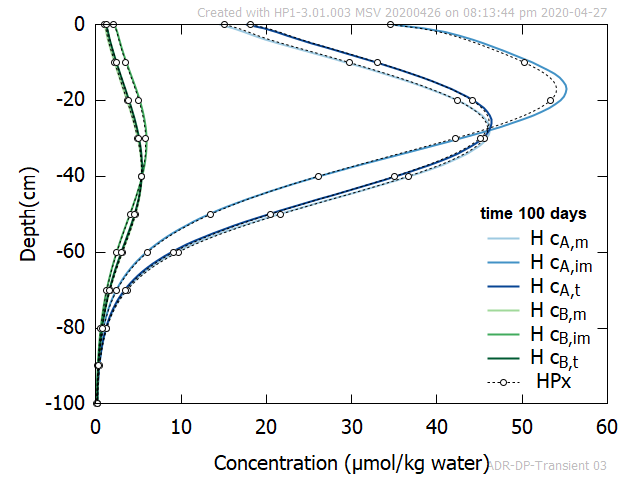
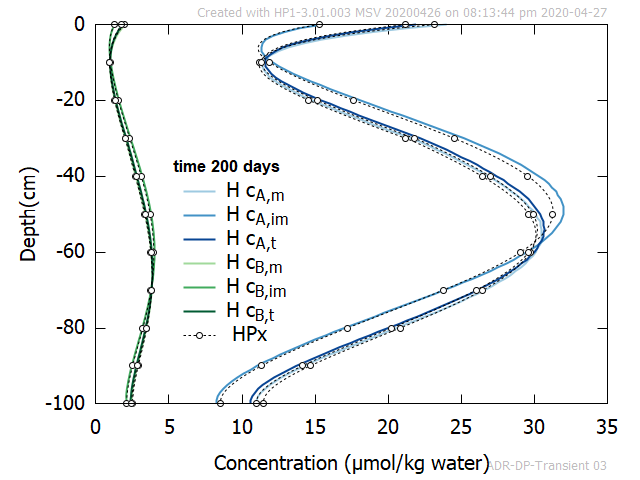
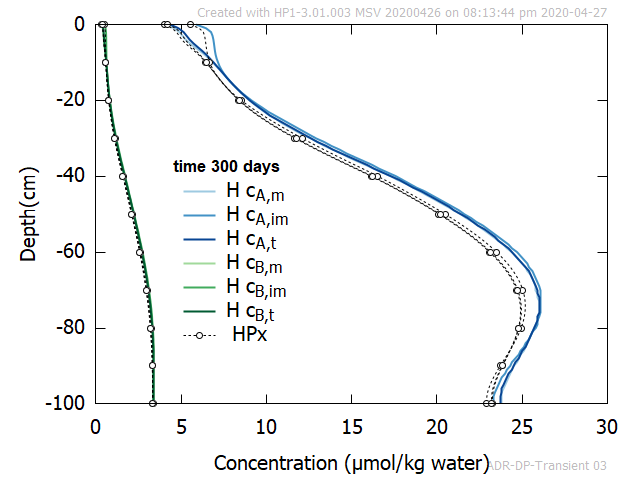
Figure 3 - Profiles at selected time of aqueous concentrations of Tracer A and B in the mobile and immobile region. Also total concentrations are given. Comparison between HPx and HYDRUS-1D.
HPx Project