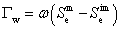Water Flow Equation

Richards' equation for variable-saturated water flow [Simunek and van Genuchten, 2008]

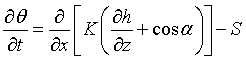
θ	water content
t	time [T]
x	spatial coordinate [L]
h	pressure head [L]
K	unsaturated hydraulic conductivity [L/T]
α	angle between flow direction and the vertical axis [°]
S	sink term [L3/L3T]

Dual porosity model for variable-saturated water flow [Simunek and van Genuchten, 2008]

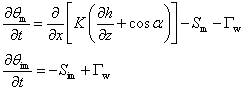
θm	water content of mobile region
θim	water content of immobile region
t	time [T]
x	spatial coordinate [L]
h	pressure head [L]
K	unsaturated hydraulic conductivity [L/T]
α	angle between flow direction and the vertical axis [°]
Sm	sink term of mobile region [L3/L3T]
S	sink term of immobile region [L3/L3T]
Γw	water transfer term between mobile and immobile region [M/L3T]

The water transfer term can be expressed in terms of fluid saturation or pressure head differences [Simunek et al., 2003]. The expression in terms of fluid saturation is given by:

ω	first-order rate coefficients [T-1]
Sem	effective fluid saturation of mobile region
Sem	effective fluid saturation of immobile region

The effective fluid saturations for the mobile and immobile regions need the saturated and residual water content of the mobile and the immobile region, respectively.